Originally posted by HuntingRoss
View Post

The method I prefer is to consider the 'time on brush' for one comm segment from 1° 'ON' to 0° 'OFF'.
For a single coil as we have been discussing in the recent past I would estimate it as so :
A = 'ON' angle
B = The angle of the comm segment
C = The angle of the brush
D = 'OFF' angle
E = The angle between P1 and P2 coil bisectors
The NSB and SSB stator bisectors are 90°
A = 'ON' angle
B = The angle of the comm segment
C = The angle of the brush
D = 'OFF' angle
E = The angle between P1 and P2 coil bisectors
The NSB and SSB stator bisectors are 90°
Plus, it would help if you assign a Letter to Stators Bisector Angle.
Where B + C = 'Time on brush'
Such that the 'OFF' angle of your proposed design (which must be a positive number variable around 20°) is -
90 - A - B - C = D
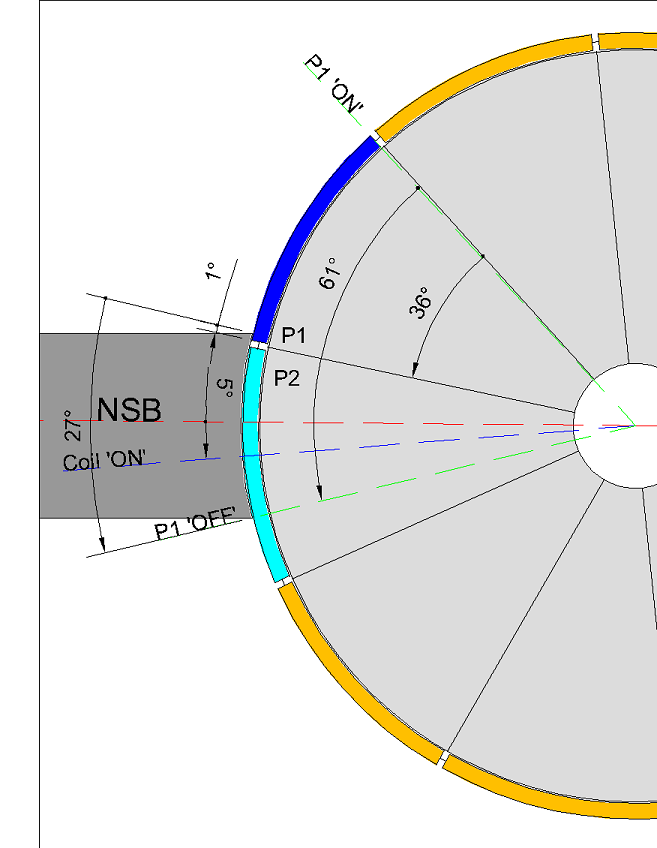
Crudely stating the comm segment as 36° and the brush as 27° and given an 'ON' angle of 8°, then
90 - 8 - 36 - 27 = 19°
More accurately from the image
90 - 8 - 61 = 21° (B + C = 61°)
To estimate the 'OFF' angle by reference to P1 and P2 together for single coils :
90 - A - C - E = D
Once again, to crudely estimate
90 - 8 - 27 - 36 = 19°
And with more accuracy
90 - 8 - 25* - 36 = 21° (* The brush angle is reduced to account for the comm segment gap of 1° plus 1° connection)
---S---
90 - A - B - C = D
Crudely stating the comm segment as 36° and the brush as 27° and given an 'ON' angle of 8°, then
90 - 8 - 36 - 27 = 19°
More accurately from the image
90 - 8 - 61 = 21° (B + C = 61°)
To estimate the 'OFF' angle by reference to P1 and P2 together for single coils :
90 - A - C - E = D
Once again, to crudely estimate
90 - 8 - 27 - 36 = 19°
And with more accuracy
90 - 8 - 25* - 36 = 21° (* The brush angle is reduced to account for the comm segment gap of 1° plus 1° connection)
---S---
Whilst you have not enlightened anyone on how to estimate the 'OFF' angle when designing your motor...
you have demonstrated the result of considering it at the design stage, below.
[IMG] [/IMG]
[/IMG]
[IMG] [/IMG]
[/IMG]
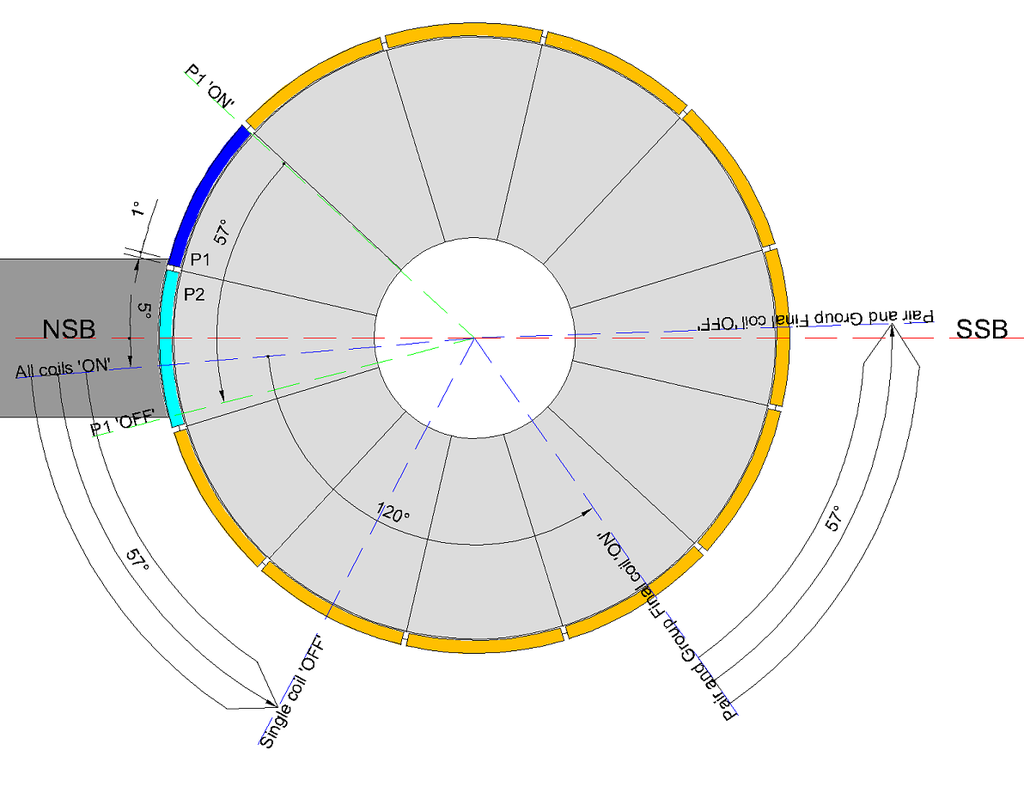
To calculate the advancement of the 'magnetic interaction angle' (coloured blue) toward the SSB, then
90° (Stator bisector) - 8° (ON angle) - 21° (OFF angle) - 36° (coil bisectors or MIA) = 25° (being the angle of the brush reduced by the comm segment of 1° plus 1° connection)
---S---
It's difficult to see the difference between one method and the other on account of there being NO difference...BUT...the difference is sufficiently large not to admit that there is ANY agreement at all.
---S---
[IMG]
 [/IMG]
[/IMG][IMG]
 [/IMG]
[/IMG]To calculate the advancement of the 'magnetic interaction angle' (coloured blue) toward the SSB, then
90° (Stator bisector) - 8° (ON angle) - 21° (OFF angle) - 36° (coil bisectors or MIA) = 25° (being the angle of the brush reduced by the comm segment of 1° plus 1° connection)
---S---
It's difficult to see the difference between one method and the other on account of there being NO difference...BUT...the difference is sufficiently large not to admit that there is ANY agreement at all.
---S---
Of course We don't have any difference NOW!!...since you have rectified your mistake...and started SUBTRACTING instead of ADDING the ON Switching Time.
Still, You have "divided" your Equations in Two Parts...and I don't understand why?...what is the point on doing so?
First You subtracted ONLY Switching Angles, meaning A,B,C & D to Stators Bisectors Angle (90º)...
Then you mixed...
90 - A - C - E = D
or...
90 - 8 - 27 - 36 = 19°
Where E is the MIA, C is Brush Angle...and A is the ON Angle or Repulse Angle.
Now, there is one "special" issue (I will better call it "Unique") in Sampojo's 10 Pole/4 Stators and 4 Pole Single Coils:
In that motor the Magnetic Interaction Angle (MIA) is exactly identical to the Commutator Segment Angle...Both being 36º...which is a very rare "Relation" to find in any other Four Stator Motor.
Meaning E=B
It tends to certain confusion when we add or subtract the number "36º" in any of above equations, no matter what letter is assigned...since the results would be the same. So in both equations is understood the results are the same.
NOW LET'S VERIFY IF YOUR EQUATIONS ABOVE HOLD TRUE IN A CONVENTIONAL MOTOR:
So let's choose Imperial, since it is a Four Stator as well, except E is not equal to B
[IMG]
 [/IMG]
[/IMG]So We have Pairs P1 and P2 each engaging Four Poles:
A = 'ON' angle= 5º
B = The angle of the comm segment = Here we use Two Segments, cause they are 56 total, each Two is then @ 12.85º round to 13º
C = The angle of the brush= 13º
D = 'OFF' angle = ?
E = The angle between P1 and P2 coil bisectors = 64.85º = Let´s round it to 65º
F=The NSB and SSB stator bisectors are 90°
Let's "clean" all this below:
A=5º
B=13º
C=13º
D= ?
E= 65º
F= 90º
So let's calculate D , and we all know D= 90-5-65 which is exactly 20º...
According to Mark's Equation:
D= 90 - A - C - E
D= 90- 5 - 13 - 65
D= 7
So, unfortunately finding D don't work on your above Equation Mark.
Now let's use your other Formula...:
90 - A - B - C = D
D= 90-5-13-13
D= 59
Close, but Nope...it can not be applied to a "Conventional" Motor Mark...so we can not use it as a "Universal Applicable Equation" am really sorry...just because We will have to keep "Hunting"...
Hopefully that clears up any confusion on why we don't agree.
Happy Hunting
mark
Happy Hunting
mark
Even though the negative results trying to calculate Imperial...I am still happy you are not adding switching angles...but deducting them...which I consider a step forward in our Timing Calculating Process.
Keep Hunting (hopefully very happy...
 )
)Ufopolitics
 :
:
Leave a comment: