Is there a quantitative difference between:
The electrical energy generated by a magnet moving relative to a conductor, and the work against the relative motion between the magnet and the conductor?
And if so, what is that difference, and why is that difference usually small?
There are actually two different definitions for the force on a magnetic dipole. One is more general than the other.
Version one: A directional derivative

Source: http://web.mit.edu/6.013_book/www/chapter11/11.8.html (Hermann A. Haus)
Version two: Gradient of a Dot Product

Source: Force on a Magnetic Dipole
They are mathematically different in a very important sense. See "The Gradient and Directional Derivative" at:
The Gradient and Directional Derivative
Here is a PDF presentation that highlights the difference between these two forces (see slide 11 of 19):
http://ictwiki.iitk.ernet.in/wiki/im...ic_Dipoles.pdf
Here is another web page highlighting the difference between these two forces:
https://www.physicsforums.com/thread...dipole.210771/
The curl of the magnetic field ∇×⃗B appears in Maxwell's Equations and is due to contributions from both conduction current and displacement current.  A rotating magnet generates changing electric fields and therefore displacement current. I would therefore argue that the part of the force involving the cross product of the magnetic moment m or μ and the curl of the magnetic field ∇×⃗B constitutes a force on the electrodynamic field itself. This condition where a magnetic dipole is at right angles to a changing electric field. This is associated with the partial time derivative of the electromagnetic field momentum (considering changes of the electric field only). One only has to look at the work of good ol' Prof. Haus (the same guy who educated Randell Mills on electromagnetic theory). Observe the paragraphs before and after equation 24 at:
A rotating magnet generates changing electric fields and therefore displacement current. I would therefore argue that the part of the force involving the cross product of the magnetic moment m or μ and the curl of the magnetic field ∇×⃗B constitutes a force on the electrodynamic field itself. This condition where a magnetic dipole is at right angles to a changing electric field. This is associated with the partial time derivative of the electromagnetic field momentum (considering changes of the electric field only). One only has to look at the work of good ol' Prof. Haus (the same guy who educated Randell Mills on electromagnetic theory). Observe the paragraphs before and after equation 24 at:
http://web.mit.edu/6.013_book/www/chapter11/11.8.html


The analogy between the polarization and magnetization was emphasized by Prof. L. J. Chu[2], who taught the introductory electrical engineering course in electromagnetism at MIT in the fifties. He derived the force law for moving magnetic charges, of which (21) is the special case for a stationary charge. His approach was soon criticized by Tellegen[3], who pointed out that the accepted model of magnetization is that of current loops being the cause of magnetization. While this in itself would not render the magnetic charge model invalid, Tellegen pointed out that the force computed from (23) in a dynamic field does not lead to (22), but to
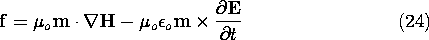
Because the force is different depending upon whether one uses the magnetic charge model or the circulating current model for the magnetic dipole, so his reasoning went, and because the circulating current model is the physically correct one, the magnetic charge model is incorrect. The issue was finally settled[4] when it was shown that the force (24) as computed by Tellegen was incorrect. Equation (23) assumes that i could be described as constant around the current loop and pulled out from under the integral. However, in a time-varying electric field, the charges induced in the loop cause a current whose contribution precisely cancels the second term in (24). Thus, both models lead to the same force on a magnetic dipole and it is legitimate to use either model. The magnetic model has the advantage that a stationary dipole contains no "moving parts," while the current model does contain moving charges. Hence the circulating current formalism is by necessity more complicated and more likely to lead to error.
Now consider what is stated in the following page of Prof. Haus' online book:
http://web.mit.edu/6.013_book/www/chapter11/11.9.html
So let's say that  is indeed the force on a magnetic dipole.
is indeed the force on a magnetic dipole.
Notice that when a magnet moves through space, the following does not necessarily have a component along the velocity:

So therefore in principle, there can be torque applied to a magnet over some angle of the magnets' rotation without implying that this dot product changes. One traditional way is to have a rotating applied magnetic field. However, it is possible for this to happen for a magnet simultaneously translating and rotating through a non-uniform magnetic field.
Enter a new development, the S.H.O. Drive:
http://sho.wiki/3d
http://sho.wiki/3d/simple
http://sho.wiki/3d/advanced
[VIDEO]https://www.youtube.com/watch?v=9QjaY7ZurtM[/VIDEO]
Links to earlier postings can be found at:
http://overunity.com/16839/s-h-o-dri...797/#msg490797
So if represents the force on a magnet, then what does
represents the force on a magnet, then what does  represent? I submit to you that it represents the energy induced via electromagnetic induction per incremental displacement w.r.t. to the sources of applied fields. So depending on the velocity between the sources of magnetic moment m or magnetization field M and magnetic flux density B or applied field H, which considers material/Langrangian derivatives (rather than the local/Eulerian kind), we may have positive changes in induced energy (i.e. accumulation of electrical energy), or we may have negative changes in induced energy (i.e. reduction of electrical energy). The evidence for this can be found in the Marinov Generator experiments:
represent? I submit to you that it represents the energy induced via electromagnetic induction per incremental displacement w.r.t. to the sources of applied fields. So depending on the velocity between the sources of magnetic moment m or magnetization field M and magnetic flux density B or applied field H, which considers material/Langrangian derivatives (rather than the local/Eulerian kind), we may have positive changes in induced energy (i.e. accumulation of electrical energy), or we may have negative changes in induced energy (i.e. reduction of electrical energy). The evidence for this can be found in the Marinov Generator experiments:
http://overunity.com/14691/the-marin...177/#msg405177
Now what does this have to do with "Space-Coupling" of magnetic fields? Observe the following page:

Note the statement: "However the gyroscopic particles comprising the magnetic fields of both the 100 lb. rotating magnet and the 4,200 lb. coil would react with one another as desired and designed by me."
The force responsible is the magnetic tension force.
It's better to use a non-Wikipedia source, and so there is:
http://www-solar.mcs.st-andrews.ac.u...r2/node15.html
To clarify the above, consider what happens when you consider the force density at a location where the current density j is equal to 0, such as large hollow volumes inside a Newman Machine (or for that matter, a S.H.O. Drive). The left side of the equation vanishes for much of the volume, where the second term on the right can be moved to the other side (with opposite sign of course), corresponding to the description in the Wikipedia article. This is the condition where "the pressure force balances the tension force so that the Lorentz force is identically zero." As you can see, this result corresponds to version one (per the beginning of this post) of the magnetic force on a dipole (Source: http://web.mit.edu/6.013_book/www/ch.../box-11.37.gif).
Now observe my recent animation:
http://sho.wiki/3d/advanced
May the Force with be you!
with be you!
[VIDEO]https://www.youtube.com/watch?v=9QjaY7ZurtM[/VIDEO][VIDEO]https://www.youtube.com/watch?v=cIaIYEAe7mo[/VIDEO]
The electrical energy generated by a magnet moving relative to a conductor, and the work against the relative motion between the magnet and the conductor?
And if so, what is that difference, and why is that difference usually small?
There are actually two different definitions for the force on a magnetic dipole. One is more general than the other.
Version one: A directional derivative

Source: http://web.mit.edu/6.013_book/www/chapter11/11.8.html (Hermann A. Haus)
Version two: Gradient of a Dot Product

Source: Force on a Magnetic Dipole
They are mathematically different in a very important sense. See "The Gradient and Directional Derivative" at:
The Gradient and Directional Derivative
Here is a PDF presentation that highlights the difference between these two forces (see slide 11 of 19):
http://ictwiki.iitk.ernet.in/wiki/im...ic_Dipoles.pdf
Here is another web page highlighting the difference between these two forces:
https://www.physicsforums.com/thread...dipole.210771/
The difference between these two force terms is using some vector relation m×(∇×⃗B). But this only vanishes if the magnetic dipole moment is parallel to the curl of B or B itself is rotationless.
 A rotating magnet generates changing electric fields and therefore displacement current. I would therefore argue that the part of the force involving the cross product of the magnetic moment m or μ and the curl of the magnetic field ∇×⃗B constitutes a force on the electrodynamic field itself. This condition where a magnetic dipole is at right angles to a changing electric field. This is associated with the partial time derivative of the electromagnetic field momentum (considering changes of the electric field only). One only has to look at the work of good ol' Prof. Haus (the same guy who educated Randell Mills on electromagnetic theory). Observe the paragraphs before and after equation 24 at:
A rotating magnet generates changing electric fields and therefore displacement current. I would therefore argue that the part of the force involving the cross product of the magnetic moment m or μ and the curl of the magnetic field ∇×⃗B constitutes a force on the electrodynamic field itself. This condition where a magnetic dipole is at right angles to a changing electric field. This is associated with the partial time derivative of the electromagnetic field momentum (considering changes of the electric field only). One only has to look at the work of good ol' Prof. Haus (the same guy who educated Randell Mills on electromagnetic theory). Observe the paragraphs before and after equation 24 at:http://web.mit.edu/6.013_book/www/chapter11/11.8.html


The analogy between the polarization and magnetization was emphasized by Prof. L. J. Chu[2], who taught the introductory electrical engineering course in electromagnetism at MIT in the fifties. He derived the force law for moving magnetic charges, of which (21) is the special case for a stationary charge. His approach was soon criticized by Tellegen[3], who pointed out that the accepted model of magnetization is that of current loops being the cause of magnetization. While this in itself would not render the magnetic charge model invalid, Tellegen pointed out that the force computed from (23) in a dynamic field does not lead to (22), but to
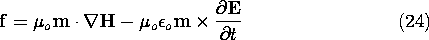
Because the force is different depending upon whether one uses the magnetic charge model or the circulating current model for the magnetic dipole, so his reasoning went, and because the circulating current model is the physically correct one, the magnetic charge model is incorrect. The issue was finally settled[4] when it was shown that the force (24) as computed by Tellegen was incorrect. Equation (23) assumes that i could be described as constant around the current loop and pulled out from under the integral. However, in a time-varying electric field, the charges induced in the loop cause a current whose contribution precisely cancels the second term in (24). Thus, both models lead to the same force on a magnetic dipole and it is legitimate to use either model. The magnetic model has the advantage that a stationary dipole contains no "moving parts," while the current model does contain moving charges. Hence the circulating current formalism is by necessity more complicated and more likely to lead to error.
http://web.mit.edu/6.013_book/www/chapter11/11.9.html
Given that the magnetizable material is made up of microscopic dipoles, each experiencing a force of the nature of (11.8.22), and that the magnetization density M is the number of these per unit volume multiplied by m, it follows from the arguments of the preceding section that the force density due to magnetization is

This is sometimes called the Kelvin magnetization force density.

This is sometimes called the Kelvin magnetization force density.
 is indeed the force on a magnetic dipole.
is indeed the force on a magnetic dipole.Notice that when a magnet moves through space, the following does not necessarily have a component along the velocity:

So therefore in principle, there can be torque applied to a magnet over some angle of the magnets' rotation without implying that this dot product changes. One traditional way is to have a rotating applied magnetic field. However, it is possible for this to happen for a magnet simultaneously translating and rotating through a non-uniform magnetic field.
Enter a new development, the S.H.O. Drive:
http://sho.wiki/3d
http://sho.wiki/3d/simple
http://sho.wiki/3d/advanced
[VIDEO]https://www.youtube.com/watch?v=9QjaY7ZurtM[/VIDEO]
Links to earlier postings can be found at:
http://overunity.com/16839/s-h-o-dri...797/#msg490797
So if
 represents the force on a magnet, then what does
represents the force on a magnet, then what does  represent? I submit to you that it represents the energy induced via electromagnetic induction per incremental displacement w.r.t. to the sources of applied fields. So depending on the velocity between the sources of magnetic moment m or magnetization field M and magnetic flux density B or applied field H, which considers material/Langrangian derivatives (rather than the local/Eulerian kind), we may have positive changes in induced energy (i.e. accumulation of electrical energy), or we may have negative changes in induced energy (i.e. reduction of electrical energy). The evidence for this can be found in the Marinov Generator experiments:
represent? I submit to you that it represents the energy induced via electromagnetic induction per incremental displacement w.r.t. to the sources of applied fields. So depending on the velocity between the sources of magnetic moment m or magnetization field M and magnetic flux density B or applied field H, which considers material/Langrangian derivatives (rather than the local/Eulerian kind), we may have positive changes in induced energy (i.e. accumulation of electrical energy), or we may have negative changes in induced energy (i.e. reduction of electrical energy). The evidence for this can be found in the Marinov Generator experiments:http://overunity.com/14691/the-marin...177/#msg405177
Finally here is a paper looking at the math behind the Marinov Generator. This takes an abitrary current loop and gives the formula for its magnetic vector potential (A) field at any point. Then for a charge that is accelerated at that point the impulse voltage induced into the loop, hence the energy taken from the current source during that impulse, is given. It is shown that this energy then resides at the charge in the form of a potential energy associated with its canonical momentum derived from the A field. That potential energy is released in the form of kinetic energy when the charge moves out of the A field. The energy balance shows that there is no OU in this situation, the final kinetic energy of the moving charge is all accounted for, but does include the energy taken from the current source. When the current loop is replaced by a permanent magnet there is apparent OU because the kinetic energy now includes that which comes from the atomic current loops, the electron spins.
* On Charge Movement through a Magnetic Vector Potential Fie….pdf (83.88 kB - downloaded 231 times.)
http://overunity.com/14691/the-marin...attach/139032/
* On Charge Movement through a Magnetic Vector Potential Fie….pdf (83.88 kB - downloaded 231 times.)
http://overunity.com/14691/the-marin...attach/139032/

Note the statement: "However the gyroscopic particles comprising the magnetic fields of both the 100 lb. rotating magnet and the 4,200 lb. coil would react with one another as desired and designed by me."
The force responsible is the magnetic tension force.
The magnetic tension force is a restoring force (SI unit: Pa·m−1) that acts to straighten bent magnetic field lines. It equals:

It is analogous to rubber bands and their restoring force. The force is directed antiradially. Although magnetic tension is referred to as a force, it is actually a pressure gradient (Pa m−1) which is also a force density (N m−3).

It is analogous to rubber bands and their restoring force. The force is directed antiradially. Although magnetic tension is referred to as a force, it is actually a pressure gradient (Pa m−1) which is also a force density (N m−3).
http://www-solar.mcs.st-andrews.ac.u...r2/node15.html
Hence, the Lorentz force may be expressed in the form

The first term represents the effect of a tension of magnitude $B^{2}/\mu $ directed parallel to ${\bf B}$. This force appears whenever the magnetic field lines are curved. The second term represents the effect of a magnetic pressure of magnitude $B^{2}/2 \mu $ per unit area that is isotropic.

The first term represents the effect of a tension of magnitude $B^{2}/\mu $ directed parallel to ${\bf B}$. This force appears whenever the magnetic field lines are curved. The second term represents the effect of a magnetic pressure of magnitude $B^{2}/2 \mu $ per unit area that is isotropic.
Now observe my recent animation:
http://sho.wiki/3d/advanced
May the Force
 with be you!
with be you![VIDEO]https://www.youtube.com/watch?v=9QjaY7ZurtM[/VIDEO][VIDEO]https://www.youtube.com/watch?v=cIaIYEAe7mo[/VIDEO]
Comment