A precessing spin is a NATURAL Faraday Disk/Homopolar generator/Unipolar Generator

[kmarinas86]

The "Potential of a Linear Quadrupole" can be found at

https://www.physicsforums.com/threads/potential-of-a-linear-quadrupole.62339/

while the "Current electric quadrupole moments of atoms and nuclei" can be found at

https://link.springer.com/article/10.1007/BF00897990

What follows from the two sources above is this:

Applying a magnetic field to magnetic material produces a spatially-variant electric potential, or should I say, dielectric potential.

For example, when we magnetize a core, we are actually inducing a magnetic precession on the electron spins in the core.



This produces a spatially-variant electric potential, like that which is produced by a rotating magnet, such as what Mr. Beaty had in mind for the magnet in the N-machine. At Mr. Beaty's article about the N-machine at

http://amasci.com/freenrg/n-mach.html

he presents the following image:



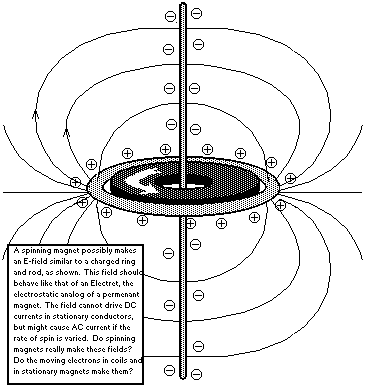
He basically had the right idea. The top answer to "What is the electric field generated by a spinning magnet?" at

https://physics.stackexchange.com/questions/6581/what-is-the-electric-field-generated-by-a-spinning-magnet

is key. It is clear from the top answer that the rotating magnet in the N-machine does produce an electric field, albeit one that does not have a curl. What is the significance of the curl-free electric field? Lenz' law deals with electric fields that have a curl, meaning the electric fields integrate to some value in a closed path:





So Lenz's law deals strictly with magnetic fields and non-conservative electric fields. However, the electric field produced by the Faraday Disk/Generator, N-machine, etc. is conservative. This conservative electric field is not produced by static electricity, however! Instead, this conservative electric field is produced by the relative motion of magnetic spins! We can switch this conservative electric field (and, by logical extension, its associated electric potential) on or off simply by changing the rate of rotation of the magnet (or in the case of Larmor precession, by changing our applied magnetic field). There is no corresponding Lenz reaction for such controllable electric fields since these electric fields are curl-free (i.e. derived from a "scalar" potential) and thus are independent of changing magnetic fields! Note the changing applied magnetic fields do produce their own distinctly different rotational electric field but that is of separate consideration from the electric fields produced from precessing spins. The braking action that occurs in typical operation of a Faraday Disk/Generator is not because of the electric force, but due to the magnetic force on the rotating conductor.

For the conservative electric field in such machines as the Faraday Disk/Generator or N-machine to do a net amount of work on charges in our circuit, the charges in our circuit should not be allowed to flow in a completely-closed path. This clearly requires atypical operation. Modern motors and generators assume that electric charge flow and/or displacement is responsible for all electric current. That is not generally true, however! The total "current" which is always closed (never divergent and never convergent) takes into account the electric displacement current that doesn't constitute a flow of charge in itself.





To ensure we have an open-pathed flow of charge in our circuit implies that we make the charge density time-variable. High voltage and high frequency across the ends of anything with a capacitance will generate some of that time-varying charge density. The faster the time-variation, the greater the associated current. As Bearden said, "Don't kill the dipole!"

Instead of building an actual Faraday Disk or N-machine, we can simply apply a magnetic field to any material with unpaired electron spins. It is not necessary to have a permeable core to induce this effect. Even if we apply a magnetic field to a permanent magnet, the spins will still undergo Larmor precession, and an electric field from the induced electric potential will emerge just like it would for the rotating magnet in a Faraday Disk/Generator, N-machine, etc..

One issue is the lifetime of the induced electric potential. Once a certain amount of precession is produced in the magnetic spins in our core or permanent magnet, it doesn't take very long for the surrounding mediums of dielectrics and conductors to "respond" to the generated electric potential by having their internal electric charges reposition. Thus, we may want to choose a material that is not very conductive such as a hard or soft ferrite magnet so the static on the surface of our coil windings (existing due to stray capacitance) will pick up more energy. The static on our windings will depend on the voltage that we apply. The current associated with that static will, in turn, depend on how quickly we vary that voltage. Whether we are dealing with a bifilar pancake coil, Tesla coil, Joe Newman coil, or what have you, ultimately the presence of "static" on our conductor surface is key.

It is important to keep in mind that the Larmor precession increases in proportion to the induced magnetic field B. So if our applied magnetic field H acts on a magnetically permeable material, the magnetic polarization M of the magnetic material will contribute to the magnetic field B responsible for the Larmor precession. What Joe Newman accomplished was done without permeable cores. He avoided permeable cores because of the hysteresis losses involved. Such losses are truly significant, especially in high-frequency applications where many common magnetic core materials do poorly at. However, if we choose a suitable ferrite core such as MnZn or NiZn, we have acceptably small hysteresis losses at the higher frequencies we are targeting. MnZn is more appropriate at AM frequencies while NiZn is more appropriate at FM frequencies. For reference, Joe Newman's air-core coils tended to be large, while being self-resonant at sub-KHz frequencies. However, the Newman machine as a whole produced copious amounts of radio frequency noise generated by the commutation arc. A paper on "Prediction of Radiated Emissions From DC Motors" can be found at

https://www.ipen.br/biblioteca/cd/ieee/1999/Proceed/00472.pdf

Apparently, when the contacts in a Newman machine are broken after the carbon brush passes the "FIRE" segment of the commutator, the coil becomes self-resonant at sub-KHZ frequencies, though some RF components may show up due to the distributed delay line that is inherent in the coil. In this process, voltage across the commutator air gap may vary widely. If the currents are in the milliamp range (or thereabouts) as is typical with Newman machines, this may result in an oscillation in the commutator spark between the glow-discharge and arc regions (i.e. the unstable glow-arc transition region) which introduces further rapid time-variation of voltage, and thus promote time-varying static charges on the windings.



Then, when the Joe Newman coil is shorted, as the rotor magnet is rotating inside it, the result is a DC-biased oscillation that ensures that the combined magnetic field (from coil and permanent magnet contributions) oscillates in a DC-biased way causing the Larmor precession frequency of the spins in the rotor magnet to reach a timewise local maximum when the AC component of the current points one way and timewise local minimum when the AC component of the current points the other way. The resultant power received by the electrical charges which shift on the coil's surface as this oscillation occurs is then what is responsible for the deep backspikes in Newman's machine whose "area" on the oscilloscope utterly dwarfs the input.



This would explain the importance of mechanical switching in Newman's machine, yet the rest of the above indicates that, indeed, it should be possible to apply a solid-state approach to harnessing the "electric field energy" associated with precessing magnetic spins.

Some information concerning Steven Mark's Toroidal Power Unit (TPU) found at

http://www.keelynet.com/news/051016k.html

seems to indicate the use of both magnetically soft and magnetically hard materials. At high frequencies, the time-varying electric potential produced by time-varying Larmor precession of the magnetic spins coupled with shifting electrostatic charge on the windings' surfaces would in principle enable copious amounts of work to be done on those surface charges, and perhaps in the TPU (too) much of that work converts into heat.

With proper optimizations maximizing the Q factor, maximizing the inductance factor, maximizing the product of voltage and resonant frequency, and reducing the random radio frequency noise, it should be possible to build a cool, small, and compact device that exploits the "electric field energy" of precessing magnetic spins with a combination of soft and/or hard ferrite magnets in the presence of a High-Voltage/High-Frequency LC tank circuit or self-resonant inductor, all while minimizing the electrical noise that we associate with "dirty electricity".

[boguslaw]

Please can you make a pdf with this info ? It's essential. IMHO magnetic field is the flow of energy and we didn't understood Faraday laws.

[Gambeir]

A pleasure to read. I make a critical comment which is instructional and not to be taken as a personal attack. It's one of my pet peeves is all. Take it for what you will. Your writing is superb and aside from a minor technical failure your logic is refined and concise. What you're after is beyond me. I haven't studied it but what you have to say is fascinating. However I can only inject a few considerations which assuredly are wildly ignorant ones.

Thank you for posting. I know how long it takes to construct something this refined and can appreciate the large amount of work it took to put this together.

To ensure we have an open-pathed flow of charge in our circuit implies that we make the charge density time-variable. High voltage and high frequency across the ends of anything with a capacitance will generate some of that time-varying charge density. The faster the time-variation, the greater the associated current. As Bearden said, "Don't kill the dipole!"

Instead of building an actual Faraday Disk or N-machine, we can simply apply a magnetic field to any material with unpaired electron spins. It is not necessary to have a permeable core to induce this effect.

You may find this useful, not sure, but thought I'd post it.

http://www.energeticforum.com/renewa...to-magvid.html
http://blog.lege.net/Mathias_Bage/GL...-annotated.pdf

Even if we apply a magnetic field to a permanent magnet, the spins will still undergo Larmor precession, and an electric field from the induced electric potential will emerge just like it would for the rotating magnet in a Faraday Disk/Generator, N-machine, etc..

Define apply; apply how? Statically or moving? The question is; is this the desired intent? I'm assuming it is.

One issue is the lifetime of the induced electric potential. Once a certain amount of precession is produced in the magnetic spins in our core or permanent magnet, it doesn't take very long for the surrounding mediums of dielectrics and conductors to "respond" to the generated electric potential by having their internal electric charges reposition.

I haven't studied so-called spintronic's but I am slowly sliding in to the ideas behind how it supposedly works. I tend to see this as a mechanical/engineering problem rectifiable through material support and or cross application of magnetic influence: My simplified view of reality no doubt.

Thus, we may want to choose a material that is not very conductive such as a hard or soft ferrite magnet so the static on the surface of our coil windings (existing due to stray capacitance) will pick up more energy. The static on our windings will depend on the voltage that we apply. The current associated with that static will, in turn, depend on how quickly we vary that voltage. Whether we are dealing with a bifilar pancake coil, Tesla coil, Joe Newman coil, or what have you, ultimately the presence of "static" on our conductor surface is key.

It is important to keep in mind that the Larmor precession increases in proportion to the induced magnetic field B. So if our applied magnetic field H acts on a magnetically permeable material, the magnetic polarization M of the magnetic material will contribute to the magnetic field B responsible for the Larmor precession. What Joe Newman accomplished was done without permeable cores. He avoided permeable cores because of the hysteresis losses involved. Such losses are truly significant, especially in high-frequency applications where many common magnetic core materials do poorly at.

However, if we choose a suitable ferrite core such as MnZn or NiZn,

OK, one of my pet peeve's comes out of scientific literature because it is meaningless pig latin approach to writing. Please avoid following the ill advised scribblings found in papers on Springer.

In summary then, it's OK to use abbreviation's, but only when they are first defined, after which the writer can precede with shorthand. A reader must be given a reference to the abbreviation and not left blind.

MnZn or NiZn? What is this? Do not expect the reader to hunt to discover what you should provide. It should read: Manganese and zinc (MnZn) or nickel-zinc (NiZn) and after which abbreviations can be used as shorthand.

This would explain the importance of mechanical switching in Newman's machine, yet the rest of the above indicates that, indeed, it should be possible to apply a solid-state approach to harnessing the "electric field energy" associated with precessing magnetic spins.

You would think that if the theory of is correct that would be the case. If it isn't then the theory is lacking or other forces are at work.

Some information concerning Steven Mark's Toroidal Power Unit (TPU) found at

http://www.keelynet.com/news/051016k.html

seems to indicate the use of both magnetically soft and magnetically hard materials. At high frequencies, the time-varying electric potential produced by time-varying Larmor precession of the magnetic spins coupled with shifting electrostatic charge on the windings' surfaces would in principle enable copious amounts of work to be done on those surface charges, and perhaps in the TPU (too) much of that work converts into heat.

With proper optimizations maximizing the Q factor, maximizing the inductance factor, maximizing the product of voltage and resonant frequency, and reducing the random radio frequency noise, it should be possible to build a cool, small, and compact device that exploits the "electric field energy" of precessing magnetic spins with a combination of soft and/or hard ferrite magnets in the presence of a High-Voltage/High-Frequency LC tank circuit or self-resonant inductor, all while minimizing the electrical noise that we associate with "dirty electricity".

This resonates with me as cross correlated to antigravitic materials in layered film.

[Gambeir]

Fascinating post: I've thought about this a little more in the context of your ending summations about what should be possible to create but has apparently seemed difficult so far.

Precession is on of the hardest things to understand because gravity is intentionally tossed in as part of cause and effect, otherwise it would be relatively easy to grasp why a top or nuclei precess by using magnetism as the motive force. Correctly understood gravity is only incoherent magnetism and nothing more. That's one reason why there is a direct and immediate correlation to magnetic influence upon matter. Virtually all matter has a magnetic field and when you bring enough of it together it will produce a magnetic field which is coherent, or alternatively the magnetic field can be produced by organized shapes, which in matter are crystalline formations.

I think of course there is some validity to the idea of electrons but it is probably an overly complicated and un-necessary artifact of misguided logic. Dielectric counterspace flows through all matter and it is seems unlikely that matter itself moves on it's own volition, but rather that the movement of dielectric energies through matter is what gives rise to what is probably an illusion of matter as spinning nuclei, and which are possibly, if not likely, the inwards spiraling's of counter-spatial energies perturbed by the existence of impeding matter, and which we are in error of mistaking for something they are not.

A magnetic field is a coherent dielectric energy field which arises out of counter-space. This medium is moving at billions of times our local light speed and is everywhere at all times. A magnetic field can be created anywhere at any time for this reason and it also appears as a holographic image in a ferocell. Any material which can conduct, which to focus or condense the magnetic field, is also viewable in a ferocell. Human blood is viewable because of the iron in it and it too has a holographic image to it.

I like the descriptions given here except for the fact that they have injected the pseudo-sciences of quantum and relativity in to the explanations.
https://mriquestions.com/why-precession.html

Strike out gravity and strike out quantum and what you then have are closer truths. Gravity does not exist and quanta is nothing more than the energies of counterspace. Since counterspace is the repository of energies entropy it's constitution is limitless. Seeking answers by enumerations of it's vast void is probably not an intelligent way to spend one's life.

If every piece of matter has dielectric paths which counterspace follows then what are we actually seeing? If electronic switching isn't possible then it must be because it isn't electrons at work.