Hi everybody:
The bob will stop at which position?
1, 2, or 3 for A and B.
The explanation and some math will elucidate us, but the poll is open to all.
Thank you
David
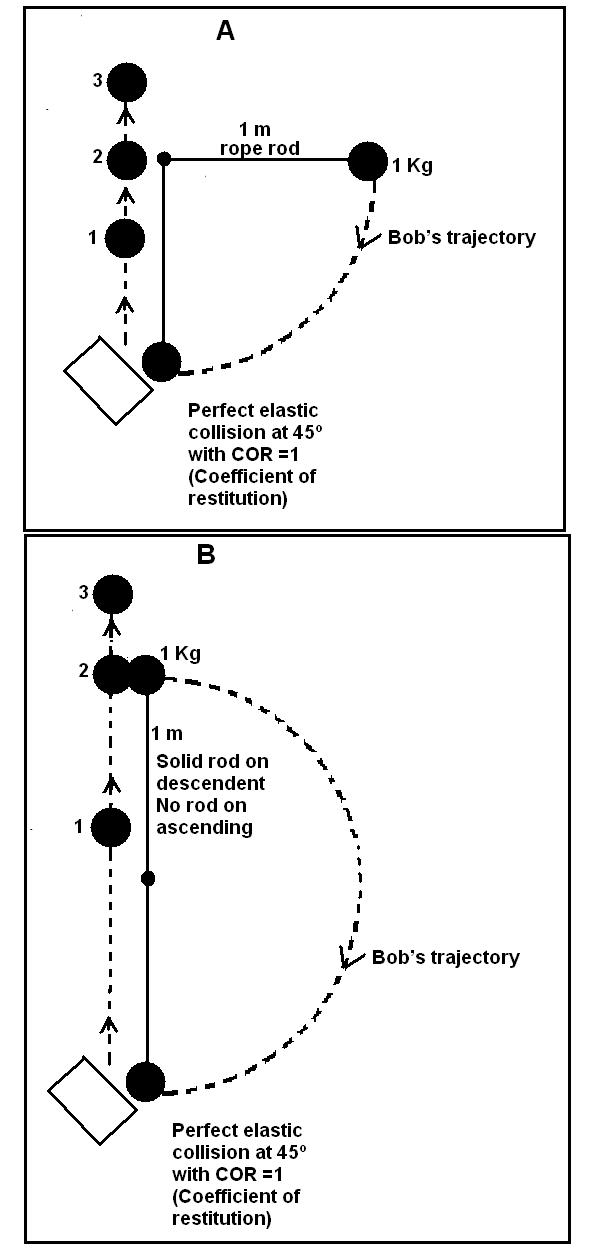
The bob will stop at which position?
1, 2, or 3 for A and B.
The explanation and some math will elucidate us, but the poll is open to all.
Thank you
David



Comment