Hi everybody:
Despite of not having much participation on my proposals, here, I am not a quitter, so, here it is another one.
It is a representation, where I have a sphere, but can be any magnetic weight that will levitate on an inductrack type rail, starting on position “1”.
At “2” one fixed rod hooks the weight and makes it reduce the radius.
At “4” unhooks the weight and slides linearly on the levitating track to “load”.
Isn’t this setup an OU?
Thank you
David
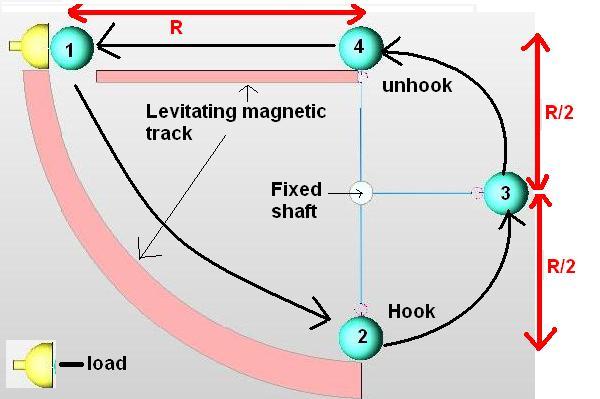
Despite of not having much participation on my proposals, here, I am not a quitter, so, here it is another one.
It is a representation, where I have a sphere, but can be any magnetic weight that will levitate on an inductrack type rail, starting on position “1”.
At “2” one fixed rod hooks the weight and makes it reduce the radius.
At “4” unhooks the weight and slides linearly on the levitating track to “load”.
Isn’t this setup an OU?
Thank you
David



 and restart the cycle.
and restart the cycle.
Comment