Hi everybody:
After learning here, http://www.energeticforum.com/renewa...tml#post106105 ,that mathematically we cannot have energy gain from an increase of a force due to an action, I come back to the “applied force” parametric pumping.
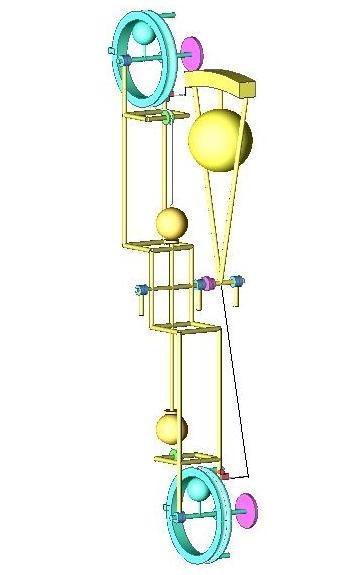
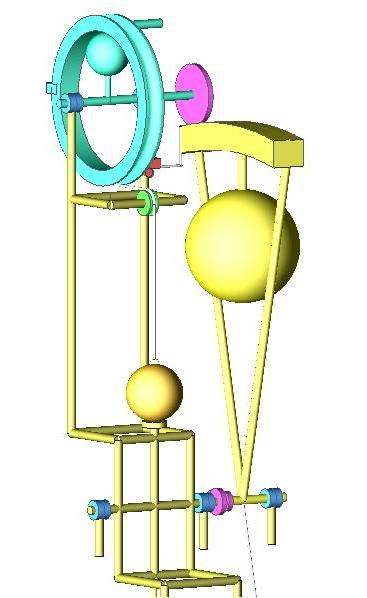
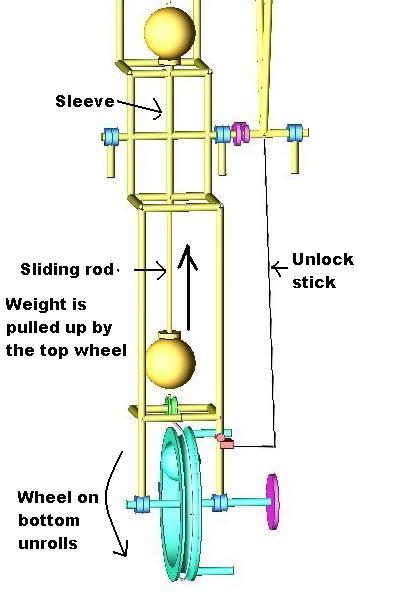
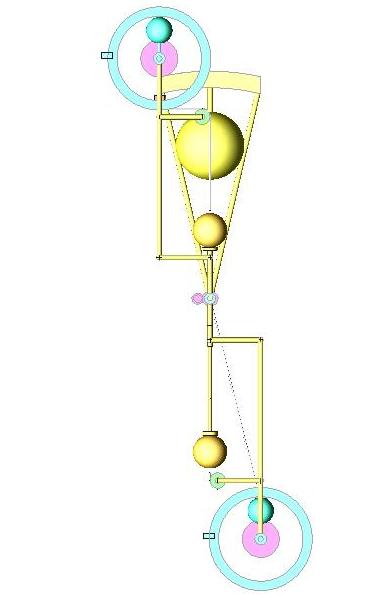
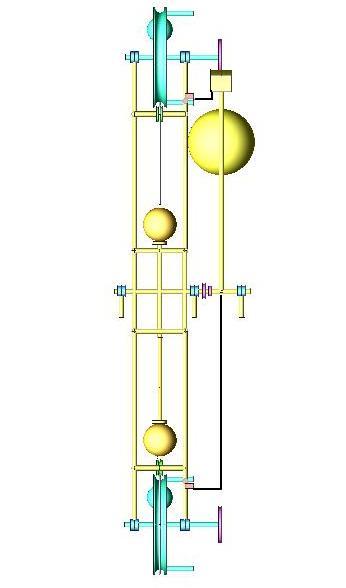
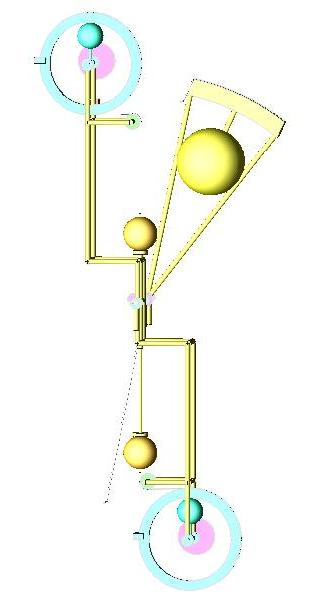
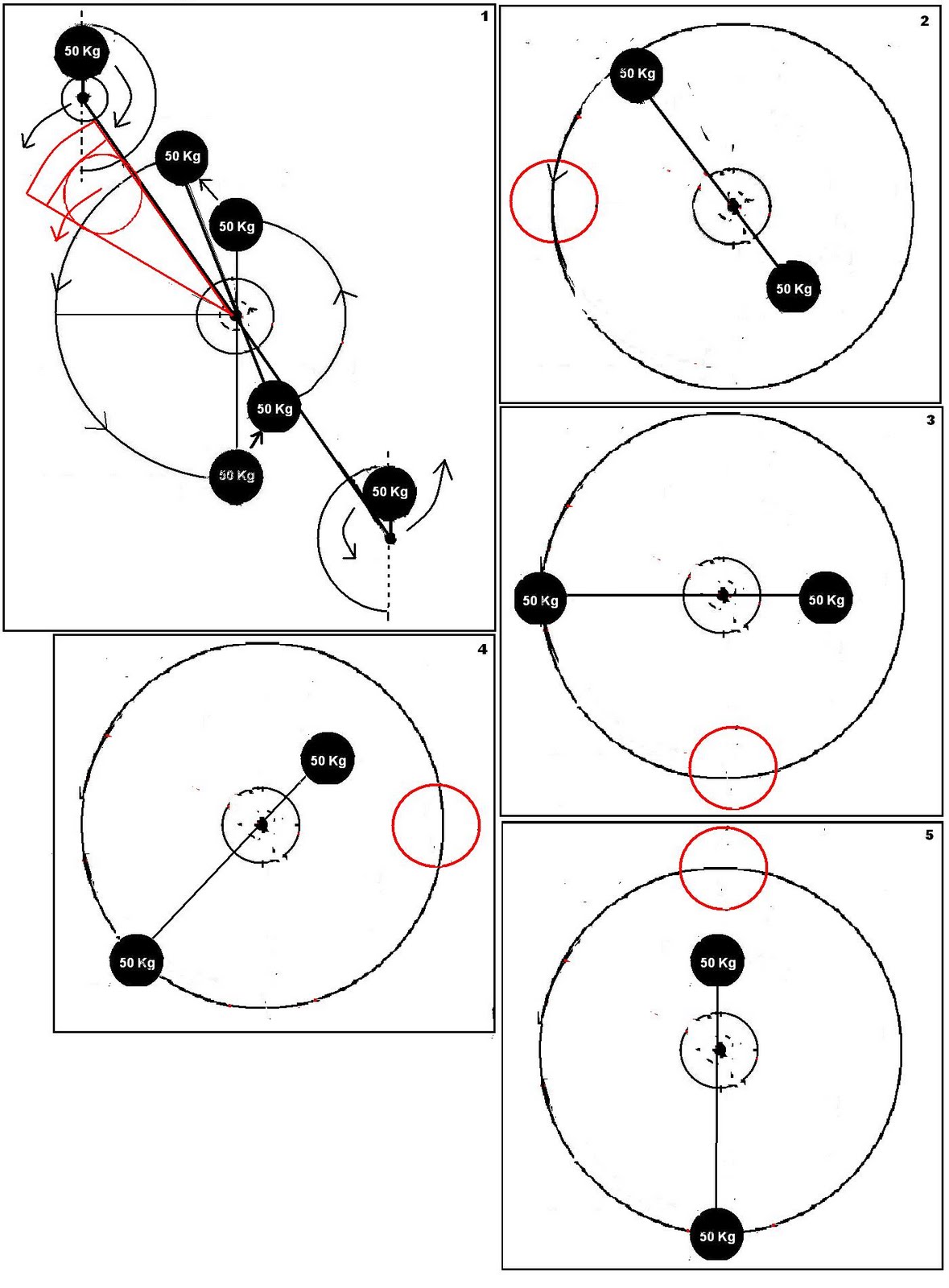
The force to change the center of mass, in a child is done along the rod, increasing the centripetal force, changing the amplitude.
The rotating wheel does pull the weights through the rod, and all the forces are on the same angular direction.
Will you guys prove mathematically that this setup will not accelerate?
Thank you
David
http://1.bp.blogspot.com/_nDqIuKRvky...XE/s1600/3.JPG
After learning here, http://www.energeticforum.com/renewa...tml#post106105 ,that mathematically we cannot have energy gain from an increase of a force due to an action, I come back to the “applied force” parametric pumping.
The force to change the center of mass, in a child is done along the rod, increasing the centripetal force, changing the amplitude.
The rotating wheel does pull the weights through the rod, and all the forces are on the same angular direction.
Will you guys prove mathematically that this setup will not accelerate?
Thank you
David
http://1.bp.blogspot.com/_nDqIuKRvky...XE/s1600/3.JPG

 which essentially states that Work equals the change in kinetic energy of a body. Now lets attach a rubber band to the pedulum. We move the pendulum the same distance as before, but we have to put more energy in to stretch the rubber band. What happens when we let go . . . does the bob stop when the rubber band is completely contracted? No, whatever inertia exists in the bob, the momentum carries it on. Assuming the bearings on our device are perfect and non friction, how much mass (inertia) can we add to our bob before the rubber band simply cannot move it? Does the MOI (Moment of Inertia) prevent any movement until the force exceeds its value?
which essentially states that Work equals the change in kinetic energy of a body. Now lets attach a rubber band to the pedulum. We move the pendulum the same distance as before, but we have to put more energy in to stretch the rubber band. What happens when we let go . . . does the bob stop when the rubber band is completely contracted? No, whatever inertia exists in the bob, the momentum carries it on. Assuming the bearings on our device are perfect and non friction, how much mass (inertia) can we add to our bob before the rubber band simply cannot move it? Does the MOI (Moment of Inertia) prevent any movement until the force exceeds its value? Can we use Inertial Gravity against Mass Gravity to break the field into non conservative parts? If so, then can we extract energy from them?
Can we use Inertial Gravity against Mass Gravity to break the field into non conservative parts? If so, then can we extract energy from them?

Comment