Originally posted by Armagdn03
View Post
what about inductive loads ?

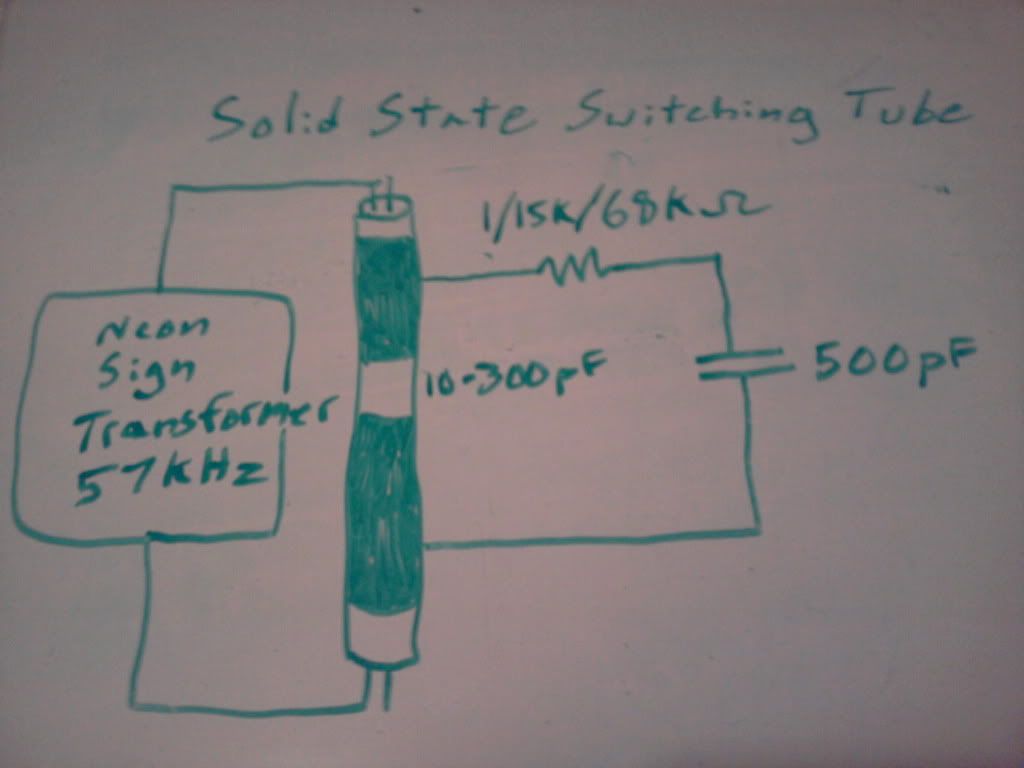
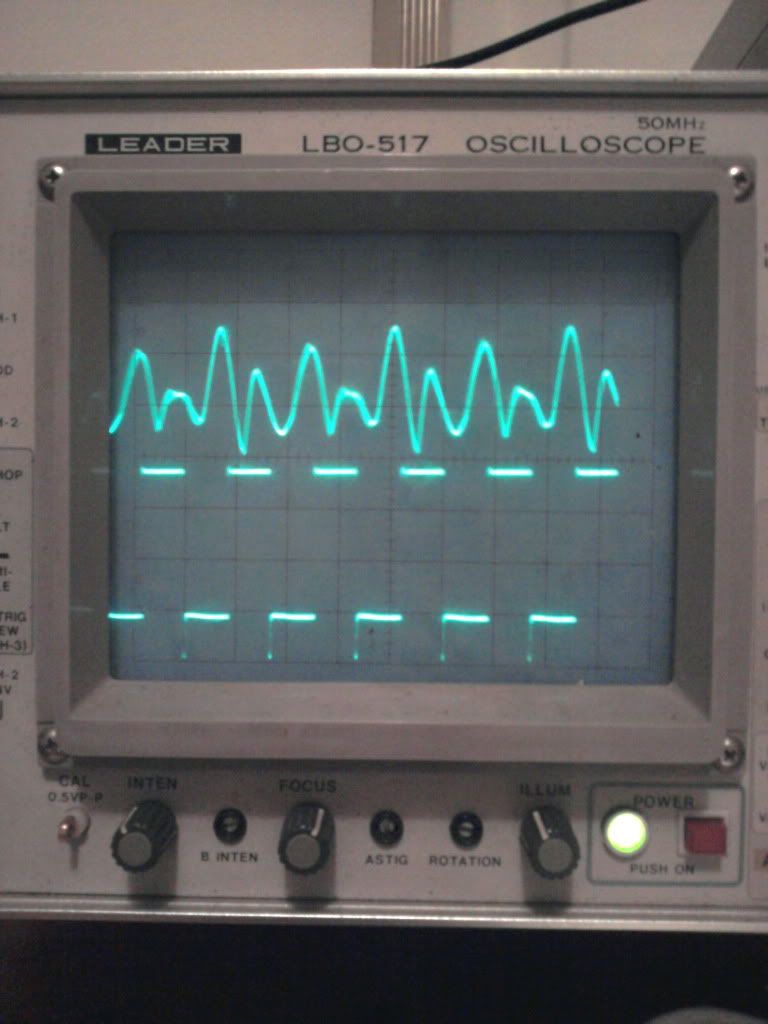



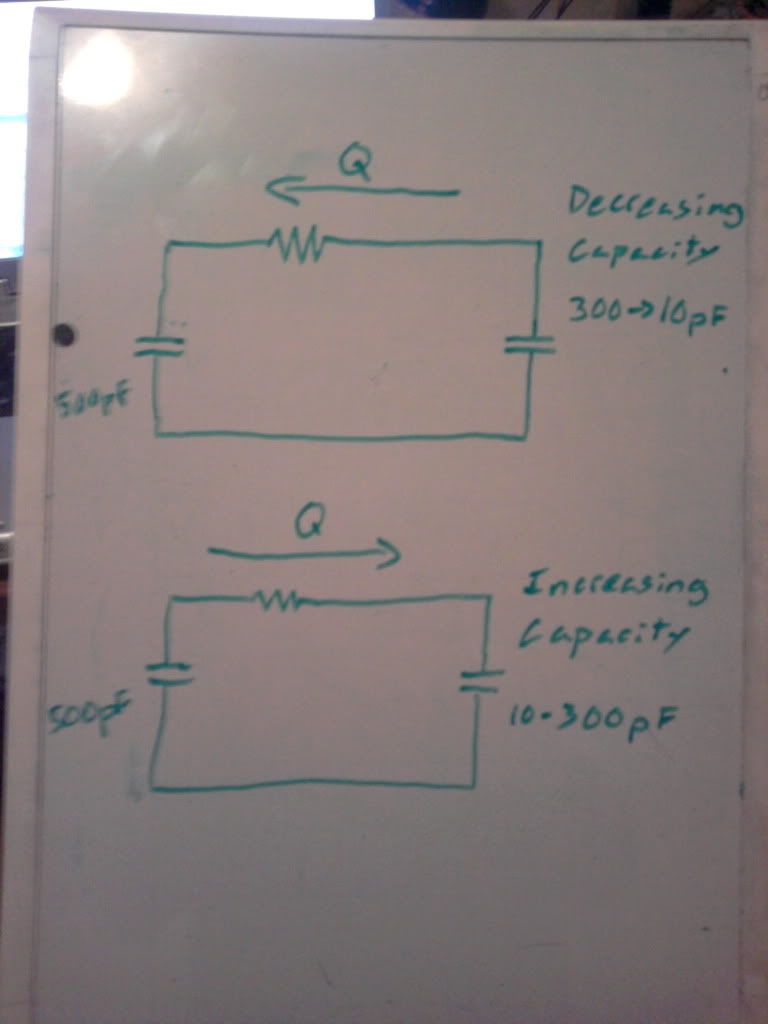
 At 500V using the calculations that I used above, I should still have 4 Watts of power dissipation in the resistor. Being a 1/4 Watt resistor, I would feel that heat, but have felt absolutely nothing.
At 500V using the calculations that I used above, I should still have 4 Watts of power dissipation in the resistor. Being a 1/4 Watt resistor, I would feel that heat, but have felt absolutely nothing.

 At 500V using the calculations that I used above, I should still have 4 Watts of power dissipation in the resistor. Being a 1/4 Watt resistor, I would feel that heat, but have felt absolutely nothing.
At 500V using the calculations that I used above, I should still have 4 Watts of power dissipation in the resistor. Being a 1/4 Watt resistor, I would feel that heat, but have felt absolutely nothing.



Comment