Hello
For simplicity lets assume a particular point in time, that the coil voltage
behaves like a step response, then the voltage of the resistor or load will vary
like this:
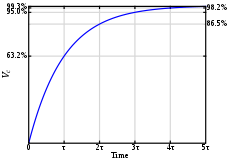
One time constant equals L/R, where L is the inductance, and R is the
resistance. There is some hesitation for the coil to provide current to the Load
and if the coil hesitates long enough so that the magnet gets past the coil,
the deceleration will decrease and as the speed or the time constant
increases it becomes acceleration.
So there are two options:
That's it!
For simplicity lets assume a particular point in time, that the coil voltage
behaves like a step response, then the voltage of the resistor or load will vary
like this:

One time constant equals L/R, where L is the inductance, and R is the
resistance. There is some hesitation for the coil to provide current to the Load
and if the coil hesitates long enough so that the magnet gets past the coil,
the deceleration will decrease and as the speed or the time constant
increases it becomes acceleration.
So there are two options:
- Increasing the speed of the Magnet, which can be done by increasing the
speed of rotation or increasing the diameter of the rotor. - Increasing the time constant, which can be done by building higher
inductance coils with less resistance, this can be better achieved by using
higher permeability core material, such as amorphous metal, which Muller was
using. Using large loads with low resistance.
That's it!







Comment