An important excerpt from the second article I linked...
I really really think we can use this even more then we already accidentally might be doing.
However, this result assumes that the ring is
purely resistive, which it is not. As it has some
self-inductance, this results in the current in the
ring lagging the applied field. The result of this
is a net upward force sufficient to levitate the ring.
If the current in the ring lags the applied field
by δ, then the upward force is proportional to
− ω sin(ωt ) cos(ωt + δ),
i.e.
12
[ω sin(2ωt) cos(δ)] + ω sin2(ωt ) sin(δ)
[cos(A + B) ≡ cosAcos B − sinAsin B].
The first term integrated over a cycle is zero,
but the second term is always positive, giving a net
upward force on the ring and hence the lift that is
observed.
This leads to the following conclusions:
(1) Lenz’s law cannot be used to explain the
motion of the ring.
(2) Faraday’s laws of induction, together with a
recognition that the ring has some
self-inductance (which leads to a phase shift
of the induced current), is the correct
explanation of the observed behaviour.
purely resistive, which it is not. As it has some
self-inductance, this results in the current in the
ring lagging the applied field. The result of this
is a net upward force sufficient to levitate the ring.
If the current in the ring lags the applied field
by δ, then the upward force is proportional to
− ω sin(ωt ) cos(ωt + δ),
i.e.
12
[ω sin(2ωt) cos(δ)] + ω sin2(ωt ) sin(δ)
[cos(A + B) ≡ cosAcos B − sinAsin B].
The first term integrated over a cycle is zero,
but the second term is always positive, giving a net
upward force on the ring and hence the lift that is
observed.
This leads to the following conclusions:
(1) Lenz’s law cannot be used to explain the
motion of the ring.
(2) Faraday’s laws of induction, together with a
recognition that the ring has some
self-inductance (which leads to a phase shift
of the induced current), is the correct
explanation of the observed behaviour.







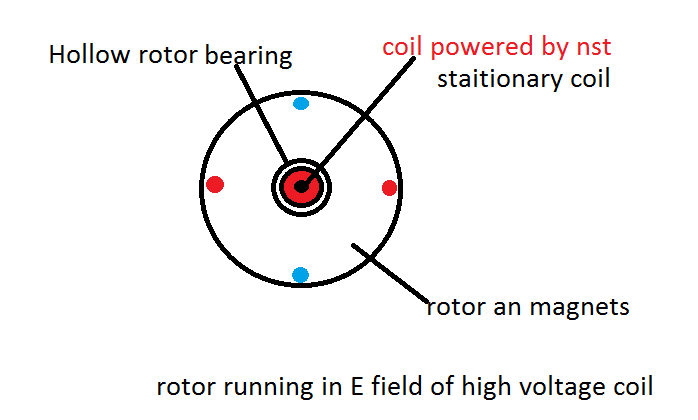
Comment