Please read this notice before re-posting this paper: Eric Dollard
---------------------------------------------------------
Chapter One
Principles of Imaginary Exponents and Logarithms
[1] Introduction
(1) In the previous writing, The Four Quadrant Representation of Electricity, a considerable portion was devoted to Versor Algebra and the distinction between the alternating and the rotating electric wave. The primary objective was to establish an understanding of the Tesla polyphase power system, or what some call his “Magnetic Vortex”. This was presented in a qualitative manner, mostly pictorial. What follows is a quantitative and rigorous treatment of this subject. It will reach to the outer limits of mathematics, the realm of what are called Imaginary Numbers. Cartesian coordinates will be lost sight of. This will finalize into engineering application, through what is known as the Method of Symmetrical Components. Unlike other works on this subject, here a solid theoretical base will be established for this method of polyphase analysis.
Nikola Tesla himself never provided a theoretical basis for his work, this was left for others. Most notable in establishing a theoretical basis for alternating current was Carl Proteus Steinmetz. In his writings a solid alternating current theory was established, this founded upon Pythagoras and Descartes. However, the work of Steinmetz was directed into alternating electric waves with little attention given to rotating electric waves. Steinmetz did not take the next step into a polyphase theory, in part because the theory of rotating electric waves exits outside the realm of the Cartesian coordinate system, which has served as the arch form of his A.C. writings. An entirely new form of mathematics is required in order to establish a functional polyphase theory.
(2) A complication exists with regard to Steinmetz in his indistinction between a vector and a versor. Oliver Heaviside had warned of this distinction, but he did not write a parable on the matter. Mathematics took a distinctly vectoral turn, with Heaviside as its champion. Steinmetz carried on from here. The only interest in versor algebra was that of Alexander MacFarlane. In the minds of the vectoralists, versors were seen as an outgrowth of quaternion, a failed system of mathematics.
Another complication in developing a working polyphase theory is the versor positions cannot be given in Cartesian coordinates, such as x and y, latitude and longitude, etc. Most polyphase systems are also not rectangular, they are triangular or hexagonal. A three phase system is triangular and requires nine coordinates for a mathematical description. The number of coordinates increases as the square of the number of phases. Common mathematics falls short in providing a usable expression for representing polyphase electric waves. This deficiency is inherent in the very foundations of mathematics and mathematicians have become content with it, however, electrical engineers cannot. This evokes the philosophy of Oliver Heaviside; mathematics is an experimental science. It is modeled upon physical observation, not petrified mathematical theory.
The complications present themselves in an inability to solve equations that are higher than the second degree. Higher orders cannot be resolved into plus or minus. Mathematics, and the human mind engendering it, are intrinsically bipolar. This condition finds a symbolic expression in the proposition put before Eve in the Garden of Eden. This is Good vs. Evil, Positive vs. Negative, Ones vs. Zeros, Us vs. Them, it is a bottomless pit. In accord, the common notions of electricity are also bipolar.
(3) The mathematics that has become the basis for electric wave theory is founded in part on the ideas of Newton in England and Leibnitz in Germany. Their ideas dealt with rates of change and accumulation, becoming known as differential and integral calculus respectively. These ideas did not get off to a good start, however. Isaac Newton was a severe paranoid, obviating any cooperative interaction. He would often conceal or deliberately confuse his work. Those he knew constantly pressed him to publish his important ideas, only to be met with rebuke for their efforts. Newton would obsessively attack anyone who worked on ideas that paralleled his own, and even attack those who had inspired the notions he held. Notable to be attacked was Leibnitz in Germany. This in turn evoked nationalistic positions which further impaired the mathematical developments.
It can verily be stated that, in part, today’s mathematics is the deformed child of a rabid paranoid. This in tandem with a Biblical curse upon mankind, the path to developing an extended mathematics for polyphase theory will be a difficult one.
Important first steps in resolving this undesirable condition were taken by Oliver Heaviside, a Prometheus of mathematics. His methodologies were not received well in the Halls of Academia, but were eagerly taken up by Carl Steinmetz and Arthur Kennelly. Out of the minds of these individuals grew modern electrical engineering, but also with their limitations. It is NOT a finality. As Heaviside stated, “There is no finality, not even with Maxwell”, but the illusion of finality is constantly put before us. Ideas must continue to advance, extending known mathematics to provide a deeper understanding of electric waves.
[2] Fundamentals of Exponentials
(1) The work of Arthur Kennelly demonstrated that considerable simplification in expressing electric waves mathematically was to be obtained by utilizing functions derived from the Napierian logarithmic base epsilon. These are known as the Hyperbolic Functions. The log base epsilon exhibits a unifying character when expressing rates of change. It is important that these ideas be completely understood before progressing into polyphase theory.
The condition that allows for a logarithmic expression of electric waves is found in that a rate of variation of an electric quantity is dependent at any moment on the quantity of electricity at that moment. Magnitude determines the rate at which it varies, the larger the magnitude, the greater the rate of change of that magnitude.
This can be given a common expression. Let us say that you have 1000 dollars in the bank at the beginning of the month, and there best be some left at the end of the month. You begin to spend the money at a certain rate in dollars per day, paying important bills. A week later you find that only 500 dollars is left in the bank. Accordingly, your rate of expenditure is reduced in reaction to the diminished funds. The end of the next weeks leaves 333 dollars in the bank, the funds still are going too fast. In reaction, the rate of expenditure is further reduced. The end of the third week leaves 250 dollars in the bank and the reaction is to even further reduce the rate of expenditure. At the end of the month 200 is left in the bank.
Your rate of expenditure decreased in proportion to the amount of money in the bank, the weekly remainder establishing a geometric regression, one half, one third, one fourth, leaving one fifth, or 20 percent of the initial money at the start of the period. At that rate of expenditure, wish varies with the amount in the bank, leaves only 20 percent of the amount, 200 dollars, at the beginning of the second month. The third month then begins with 40 dollars. Only after an infinite number of months is nothing left in the bank. This relation can be expressed in a mathematical form by


A is the ratio of the end of month amount, to the beginning of the month amount, over a logarithmic period of one month.
α is the ratio of the end of month amount, to the beginning of the month amount, over a logarithmic period of one month.
n is the number of months.
Substituting the bank analog into this expression gives for the first month
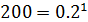 x 1000
x 1000And for the second month
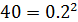 x 1000
x 1000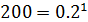 x 1000
x 1000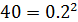 x 1000
x 1000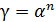
where the number of (monthly) periods, n, is called the logarithm of gamma (
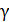 ) to base α. Base a constitutes α geometric ratio, a pure numeric.
) to base α. Base a constitutes α geometric ratio, a pure numeric. Electricity and its rates of variation operate in accord with this kind of exponential function. For the bank analog the rates were incremental, based upon human emotion, etc. For the natural decrement of electricity the function is continuous. The log base is a comparison, or ratio of magnitudes, devoid of the dimensions of these magnitudes. The log base is a number in the Pythagorean understanding.


Leave a comment: