DC Transmission Line II (5-?)
Wow, the previous post sure puts my puny efforts in perspective.
Dec. 3 - Since no one has yet pointed out my lapses I will fix them here in italics.
I am going to try a more generic approach to balancing the forces in the transmission line.
Equation 40 on page 138 of the “Discharges book” gives an equivalency between the L and C in a given transmission line:
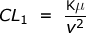
Where C is the capacitance in farads per cm and L1 is inductance external to the conductors in henrys per cm. k is the specific capacitance or permittivity and µ the permeability of the medium. v is the velocity of light in cm per second. You can calculate L from C and C from L:
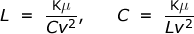
Starting from the dielectric and magnetic energy of the transmission line circuit. Length is the length of the line in cm.

The force is the change in energy with respect to changes in s. Note that s being measured in a direction parallel to the direction of the force. Set the sum of the forces to zero.

The Lengths cancel out. Next substitute L for C and apply chain rule. The derivatives of L will cancel out. Then substitute C for L.
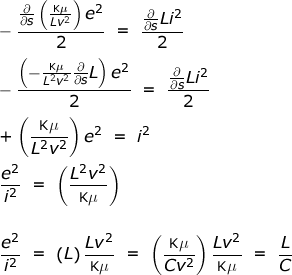
Taking the square root of both sides:

which has just been shown to be the same ratio of e to i which causes the magnetic and dielectric forces to balance.
Wow, the previous post sure puts my puny efforts in perspective.
Dec. 3 - Since no one has yet pointed out my lapses I will fix them here in italics.
I am going to try a more generic approach to balancing the forces in the transmission line.
Equation 40 on page 138 of the “Discharges book” gives an equivalency between the L and C in a given transmission line:
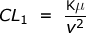
Where C is the capacitance in farads per cm and L1 is inductance external to the conductors in henrys per cm. k is the specific capacitance or permittivity and µ the permeability of the medium. v is the velocity of light in cm per second. You can calculate L from C and C from L:
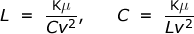
Starting from the dielectric and magnetic energy of the transmission line circuit. Length is the length of the line in cm.

The force is the change in energy with respect to changes in s. Note that s being measured in a direction parallel to the direction of the force. Set the sum of the forces to zero.

The Lengths cancel out. Next substitute L for C and apply chain rule. The derivatives of L will cancel out. Then substitute C for L.
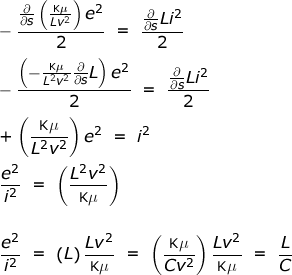
Taking the square root of both sides:

which has just been shown to be the same ratio of e to i which causes the magnetic and dielectric forces to balance.



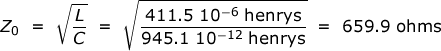
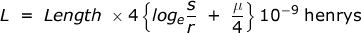

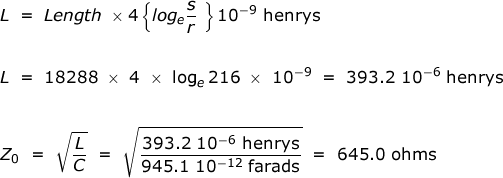

Comment