Hi all,
As you know I'm working on a longitudinal moonbounce project and am currently calculating my antenna. I found out that the transverse surface wave across the sphere can be expressed with the theoretical formula for Schumann resonance:
Schumann resonances - Wikipedia, the free encyclopedia
f_n= c/(2*pi*r) * sqrt(n(n+1))
So, I compared the Schuman formula with the formula for resonance in a string, basically a 1/2 lambda resonance with closed ends:
f_n = (n * c_l)/ 2L
Since n(n +1) equals 6 for n=2, we get:
c_l / (4 * r) = c_t / (2 * pi * r) * sqrt(6)
c_l = 2/pi * sqrt(6) * c_t
So, now we have a theoretical derivation for the longitudinal wave speed, which turns out to be just a tiny bit lower than Eric's pi/2...


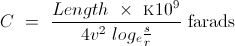
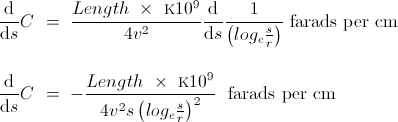

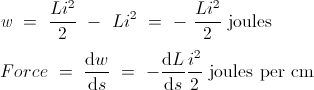



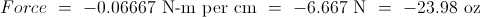


Leave a comment: